I recently have been spending a fair amount of time on CodeWars. Many of the katas on the site are based around math problems. My mathematic skills are not great, so in an attempt to make it easier to tackle these problems I have collected the following notes:
Difference between Algebra and Calculus
Algebra & calculus are two different branches of mathematics.
- Algebra is the simpler of the two and can be used in everyday life. It deals with operations and relations of mathematics and their respective rules.
- Calculus is more complex and has its applications in professional fields only. Calculus is the study of change. It deals with functions, limits, derivatives, integrals & infinite series.
Read more on the differences between the two fields.
Exponents and PowerOf
When we write:
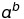
We say that a is the “base”, b is the “exponent”, and the whole thing is “a power of b”.
Inversing Exponents
To inverse an exponent you need to use logarithms. For the following exponent (where b > 0) :
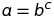
We could rewrite it as follows :
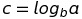
Another way to represent the relationship between exponents and logarithms is as follows :
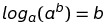
Read more about inversing exponenets.
Calculate a PowerOf without using libraries
const powerOf = (n, y) => {
let x = n;
while (x % y == 0) x = x / y;
return x == 1;
}
Exponential Growth & Decay
Assume Foo grew by 15% every year. Foo would be experiencing exponential growth. Exponential growth can be represented using the following equation :
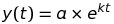
- where y(t) is a value at time “t”
- a = value at the start
- k = rate of growth (when > 0) or decay (when < 0)
- t = time
Math Is Fun Explanation
Wiki Explanation
Compounded Interest
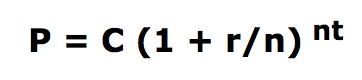
where
P = future value
C = initial deposit
r = interest rate (expressed as a fraction: eg. 0.06)
n = # of times per year interest is compounded
t = number of years invested
The compound interest equation
The relationship between exponential growth and compound interest
Averages
Simple formula for calculating averages if you know the total length
sum of vals / number of vals
Formula for calculating the running average (useful if you don’t know the total length)
- Multiply the current average by the current number of values in your collection
- Add the new number (creating a weighted sum)
- Divide by the new number of values in the collection
For example : Multiplying the average of the first 10 by 10 and then adding the 11th (creating a weighted sum) and then dividing by 11
const average = (arr) => arr.reduce((t,c,i) => ((t * i) + c) / (i + 1),0);
Pronic Numbers
A pronic number, oblong number, rectangular number or heteromecic number, is a number which is the product of two consecutive integers, that is, n(n + 1).
public class Kata
{
public static bool IsPronic(int n)
{
return Math.Sqrt(1 + 4 * n) % 1 == 0;
}
}
Triangular, Polygonal Numbers
A Triangular number is the term for a factorial type operation, but with summation instead of products?
var triangular = (n*(n+1)) / 2;
Triangular Numbers
Polygonal Numbers
Triangle Inequality Theorem
Triangle Inequality Theorem, which states that the sum of two side lengths of a triangle is always greater than the third side. If this is true for all three combinations of added side lengths, then you will have a triangle.
Permutations vs Combinations
Combinations if order DOES NOT matter.
Permutations if order DOES matter.
Permutations
2 Types:
- Repetition is allowed (n^r times)
- Repetition is NOT allowed (n! / (n - r)!)
n^r
Imagine you have a lock with 10 numbers on it from 0..9 and you have to choose 3 of them.
10^3 = 1000 permutations
n! / (n - r)!
What order could 16 pool balls be in?
- Our first choice has 16 possibilities.
- Our second choice has 15 possibilities.
- Our third choice has 14 possibilities.
- etc.
Combinations
2 Types:
- Repetition is allowed
- Repetition is NOT allowed
When repetition is allowed:
(n + r - 1)! / r! (n - 1)!
where n is the number of things to choose from, and we choose r of them.
When repetition is NOT allowed:
n! / (r! * (n - r)!)
where n is the number of things to choose from, and we choose r of them.
Combinations and Permutations
Combination Calculator
Factorial
Read shmoop’s explanation on factorials & permutations for a humorous and understandable explanation of factorials.
Recursive Factorial
Calculating factorial can be done as follows in JavaScript…
const fact = (n) => {
if (n === 0) return 1;
if (n < 0 ) return undefined;
for(var i = n; --i; ) {
n *= i;
}
return n;
}
Or…
function factorial(n) {
return n>=0 ? n ? n*factorial(n-1) : 1 : null;
}
Non-recursive Factorial
Since an integers overflow on anything bigger than 12!, non-recursive factorials can often be done using look up tables…
public int factorial(int n) {
int[] fact = {1, 1, 2, 6, 24, 120, 720, 5040, 40320,
362880, 3628800, 39916800, 479001600};
return fact[n];
}
Sum of multiples
Sn = (n/2) * (a1 + an)
Sn = the sum of the n terms in the sequence. n = number of terms in the sequence a1 = the first term in the sequence. an = the nth term in the sequence.
Calculating the nth root of a number
Get the nth root of a number using JavaScript
Use the following:
Math.pow(n, 1/root);
e.g.
Math.pow(25, 1/2) == 5
Calculating Prime
When calculating primes you do not need to traverse every single number. You only need to check up to the sqrt of a number.
function isPrime(x) {
let xSqrt = Math.sqrt(x);
if (x < 2) return false;
if (x === 2) return true;
for(let i = 3; i <= xSqrt; i++) {
if(x % i === 0) return false;
}
return true;
}
Alternative…
def isPrime2(n):
if n==2 or n==3: return True
if n%2==0 or n<2: return False
for i in range(3,int(n**0.5)+1,2): # only odd numbers
if n%i==0:
return False
return True
Or…
def isprime(n):
return n > 1 and all(n % i for i in xrange(2, n))
Lowest Common Denominator / Greatest Common Denominator
var gcd = function(a, b) {
if ( ! b) {
return a;
}
return gcd(b, a % b);
};
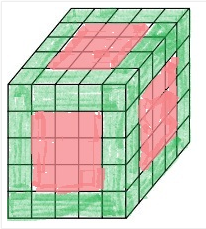
Cutting Cubes
If you have a cube and you cut it once across all 3 dimensions, how many different types of cubes will you have? Do we have a formula for calculating this for any number of cuts across all 3 dimensions?
If we cut a cube into x number of halves, the total number of small cubes is (no. of halves) to the power of 3.
const totalCubes = (cuts) => Math.pow(cuts, 3);
If we painted the cube a color, and then cut it into smaller cubes, what are the different types of cubes we will have?
1) Central cubes that are not painted
2) Cubes that are painted on only one side
3) Cubes that are painted on 2 sides
4) Cubes that are painted on 3 sides
Cubes that are not painted
Take the number of cuts, visualize on one plain so that you can see rows and columns - we call this a face.
The total number of small cubes that are unpainted would be the (number of cuts - 2) ^ 3
Cubes that are painted on only one side
Number of faces * central cubes
Cubes that are painted on only two sides
Number of 2 sides in one face * 3
Cubes that are painted on only three sides
This will be the corners of the original cube, which will always be 8
Worked Example
If we cut a cube into 5 number of halves, the total number of small cubes are as follows:
Cubes that are not painted = (5 - 2)^3 = 27
Cubes that are painted on one side = (6 * 9) = 54
Cubes that are painted on two sides = (3 * 12) = 36
Cubes that are painted on three sides = 9
Total Cubes are 125
Square Root
Calculate Square Root
Using Newton’s Formula - see more
function squareRoot(n) {
let curSqrtApprox = guess(n);
do {
let prevSqrtApprox = curSqrtApprox;
curSqrtApprox = newtonApprox(curSqrtApprox, n);
if (curSqrtApprox === prevSqrtApprox) return curSqrtApprox;
} while (0 !== 1)
}
const adjustPrecision = (x) => Number(x.toFixed(5));
const newtonApprox = (x, ori) => adjustPrecision(x - (sqrfun(x, ori) / derivative(x)));
const sqrfun = (x, ori) => (x * x) - ori;
const derivative = (x) => 2 * x;
const guess = (x) => x / 2;
Another approach…
const squareRoot = x => +((Math.cos(Math.asin((((x+1)/2)-1)/((x+1)/2)))*((x+1)/2)).toFixed(5))
Square Root using Exponents
To get the root of a number - for instance the square root can be calculated as follows
// square root of 9
let result = Math.pow(9, 1/2);
or
sqrt = n ** 0.5
You can apply the same approach to any root, the cubed root can be calculated as follows
// cubed root of 9
let result = Math.pow(9, 1/3);
Distance / Length of a line
Length of Line Segment (Distance) explained
Find equation of straight line given 2 points
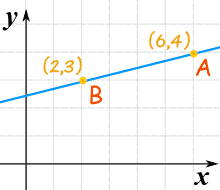
Find the slope using the following:
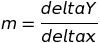
Find the equation from two points:
Use “point-slope” formula
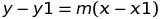
Or, another way to format it would be to use the “Slope-Intercept” form:
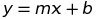
Remainder
Calculate the remaineder without using the modulous operator…
const remainder = (D , d) => d == 0 ? "NaN" : D - (Math.floor(D / d) * d);

